数据结构面试题:树与图
1. 实现一个函数,检查二叉树是否平衡
在这个问题中,平衡树的定义如下:任意一个结点,其两棵子树的高度差不超过1。
还算幸运,此题至少明确给出了平衡树的定义:任意一个结点,其两棵子树的高度差不大于1。根据该定义可以得到一种解法,即直接递归访问整棵树,计算每个结点两棵子树的高度。
public static int getHeight(TreeNode root) {
if (root == null)
return 0; // 终止条件
return Math.max(getHeight(root.left),
getHeight(root.right)) + 1;
}
public static boolean isBalanced(TreeNode root) {
if (root == null)
return true; // 终止条件
int heightDiff = getHeight(root.left) - getHeight(root.right);
if (Math.abs(heightDiff) > 1) {
return false;
} else { // 递归
return isBalanced(root.left) && isBalanced(root.right);
}
}
虽然可行,但效率不太高,这段代码会递归访问每个结点的整棵子树。也就是说,getHeight会被反复调用计算同一个结点的高度。因此,这个算法的时间复杂度为O(N log N)。
我们可以删减部分getHeight调用。
仔细查看上面的方法,你或许会发现,getHeight不仅可以检查高度,还能检查这棵树是否平衡。那么,我们发现子树不平衡时又该怎么做呢?直接返回-1。
改进过的算法会从根结点递归向下检查每棵子树的高度。我们会通过checkHeight方法,以递归方式获取每个结点左右子树的高度。若子树是平衡的,则checkHeight返回该子树的实际高度。若子树不平衡,则checkHeight返回-1。checkHeight会立即中断执行,并返回-1。
下面是该算法的实现代码。
public static int checkHeight(TreeNode root) {
if (root == null) {
return 0; // 高度为0
}
/* 检查左子树是否平衡*/
int leftHeight = checkHeight(root.left);
if (leftHeight == -1) {
return -1; // 不平衡
}
/* 检查左子树是否平衡*/
int rightHeight = checkHeight(root.right);
if (rightHeight == -1) {
return -1; // 不平衡
}
/* 检查当前结点是否平衡*/
int heightDiff = leftHeight - rightHeight;
if (Math.abs(heightDiff) > 1) {
return -1; // 不平衡
} else {
/* 返回高度*/
return Math.max(leftHeight, rightHeight) + 1;
}
}
public static boolean isBalanced(TreeNode root) {
if (checkHeight(root) == -1) {
return false;
} else {
return true;
}
}
这段代码需要O(N)的时间和O(H)的空间,其中H为树的高度。
2. 创建一棵高度最小的二叉查找树
给定一个有序整数数组,元素各不相同且按升序排列。
要创建一棵高度最小的树,就必须让左右子树的结点数量越接近越好。也就是说,我们要让数组中间的值成为根结点,这么一来,数组左边一半就成为左子树,右边一半成为右子树。
然后,我们继续以类似方式构造整棵树。数组每一区段的中间元素成为子树的根结点,左半部分成为左子树,右半部分成为右子树。
一种实现方式是使用简单的root.insertNode(int v)方法,从根结点开始,以递归方式将值v插入树中。这么做的确能构造最小高度的树,但效率并不是太高。每次插入操作都要遍历整棵树,时间开销为O(N log N)。
另一种做法是以递归方式运用createMinimalBST方法,从而消除部分多余的遍历操作。这个方法会传入数组的一个区段,并返回最小树的根结点。
该算法简述如下。
- 将数组中间位置的元素插入树中。
- 将数组左半边元素插入左子树。
- 将数组右半边元素插入右子树。
- 递归处理。
下面是该算法的实现代码。
TreeNode createMinimalBST(int arr[], int start, int end) {
if (end < start) {
return null;
}
int mid = (start + end) / 2;
TreeNode n = new TreeNode(arr[mid]);
n.left = createMinimalBST(arr, start, mid - 1);
n.right = createMinimalBST(arr, mid + 1, end);
return n;
}
TreeNode createMinimalBST(int array[]) {
return createMinimalBST(array, 0, array.length - 1);
}
尽管这段代码看起来不是特别复杂,但在编写过程中很容易犯了差一错误(off-by-one)。对这部分代码,务必进行详尽测试。
3. 创建含有一颗二叉树某一深度上所有结点的链表
给定一棵二叉树,设计一个算法,创建含有某一深度上所有结点的链表,比如,若一棵树的深度为D,则会创建出D个链表。
乍一看,你可能认为这个问题需要一层一层逐一遍历,但其实并无必要。你可以用任意方式遍历整棵树,只要记住结点位于哪一层即可。
我们可以将前序遍历算法稍作修改,将level + 1传入下一个递归调用。下面是使用深度优先搜索的实现代码。
void createLevelLinkedList(TreeNode root,
ArrayList<LinkedList<TreeNode>> lists, int level) {
if (root == null)
return; // 终止条件
LinkedList<TreeNode> list = null;
if (lists.size() == level) { // 该层不在链表中
list = new LinkedList<TreeNode>();
/* 以中序遍历所有层级,因此,若这是第一次
* 访问第i层,则表示我们已访问过第0到i-1层。
* 因此,我们可以安全地将这一层加到链表
* 末端。*/
lists.add(list);
} else {
list = lists.get(level);
}
list.add(root);
createLevelLinkedList(root.left, lists, level + 1);
createLevelLinkedList(root.right, lists, level + 1);
}
ArrayList<LinkedList<TreeNode>> createLevelLinkedList(
TreeNode root) {
ArrayList<LinkedList<TreeNode>> lists =
new ArrayList<LinkedList<TreeNode>>();
createLevelLinkedList(root, lists, 0);
return lists;
}
另一种做法是对广度优先搜索稍加修改,即从根结点开始迭代,然后第2层,第3层,等等。
处于第i层时,则表明我们已访问过第i-1层的所有结点。也就是说,要得到i层的结点,只需直接查看i-1层结点的所有子结点即可。
下面是该算法的实现代码。
ArrayList<LinkedList<TreeNode>> createLevelLinkedList(TreeNode root) {
ArrayList<LinkedList<TreeNode>> result =
new ArrayList<LinkedList<TreeNode>>();
/* 访问根结点*/
LinkedList<TreeNode> current = new LinkedList<TreeNode>();
if (root != null) {
current.add(root);
}
while (current.size() > 0) {
result.add(current); // 加入上一层
LinkedList<TreeNode> parents = current; // 转到下一层
current = new LinkedList<TreeNode>();
for (TreeNode parent : parents) {
/* 访问子结点*/
if (parent.left != null) {
current.add(parent.left);
}
if (parent.right != null) {
current.add(parent.right);
}
}
}
return result;
}
你可能会问,这两种解法哪一种效率更高?两者的时间复杂度皆为O(N),那么空间效率呢?乍一看,我们可能会以为第二种解法的空间效率更高。
在某种意义上,这么说也对。第一种解法会用到O(log N)次递归调用(在平衡树中),每次调用都会在栈里增加一级。第二种解法采用迭代遍历法,不需要这部分额外空间。
不过,两种解法都要返回O(N)数据,因此,递归实现所需的额外O(log N)空间,跟必须传回的O(N)数据相比,并不算多。虽然第一种解法确实使用了较多的空间,但从大O记法的角度来看,两者效率是一样的。
4. 实现一个函数,检查一棵二叉树是否为二叉查找树
此题有两种不同的解法。第一种是利用中序遍历,第二种则建立在left <= current < right这项特性之上。
解法1:中序遍历
看到此题,闪过的第一个想法可能是中序遍历,将所有元素复制到数组中,然后检查该数组是否有序。这种解法要多用一点内存,大部分情况下都没问题。
唯一的问题在于,它无法正确处理树中的重复值。例如,该算法无法区分下面这两棵树(其中一棵是无效的),因为两者的中序遍历结果相同。
Valid BST [20.left = 20]
Invalid BST [20.right = 20]
不过,要是假定这棵树不得包含重复值,那么这种做法还是行之有效的。该方法的伪码大致如下:
public static int index = 0;
public static void copyBST(TreeNode root, int[] array) {
if (root == null)
return;
copyBST(root.left, array);
array[index] = root.data;
index++;
copyBST(root.right, array);
}
public static boolean checkBST(TreeNode root) {
int[] array = new int[root.size];
copyBST(root, array);
for (int i = 1; i < array.length; i++) {
if (array[i] <= array[i - 1])
return false;
}
return true;
}
注意,这里必须记录数组在逻辑上的“尾部”,用它来分配空间以储存所有元素。
仔细审视这个解法,我们就会发现代码中的数组实无必要。除了用来比较某个元素和前一个元素,别无他用。那么,为什么不在进行比较时,直接记下最后的元素?
下面是该算法的实现代码。
public static int last_printed = Integer.MIN_VALUE;
public static boolean checkBST(TreeNode n) {
if (n == null)
return true;
// 递归检查左子树
if (!checkBST(n.left))
return false;
// 检查当前结点
if (n.data <= last_printed)
return false;
last_printed = n.data;
// 递归检查右子树
if (!checkBST(n.right))
return false;
return true; // 全部检查完毕
}
要是不喜欢使用静态变量,可以稍作修改,使用包裹类存放这个整数值,如下所示:
class WrapInt {
public int value;
}
或者,若用C++或其他支持按引用传值的语言实现,就可以这么做。
解法2:最小/最大法
第二种解法利用的是二叉查找树的定义。
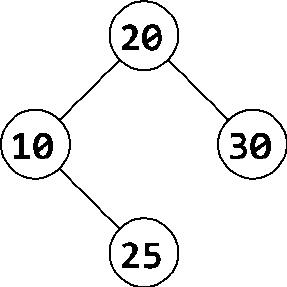
一棵什么样的树才成其为二叉查找树?我们知道这棵树必须满足以下条件:对于每个结点,left.data <= current.data < right.data,但是这样还不够。试看下面这棵小树:
尽管每个结点都比左子结点大,比右子结点小,但这显然不是一棵二叉查找树,其中25的位置不对。
更准确地说,成为二叉查找树的条件是:所有左边的结点必须小于或等于当前结点,而当前结点必须小于所有右边的结点。
利用这一点,我们可以通过自上而下传递最小和最大值来解决这个问题。在迭代遍历整个树的过程中,我们会用逐渐变窄的范围来检查各个结点。
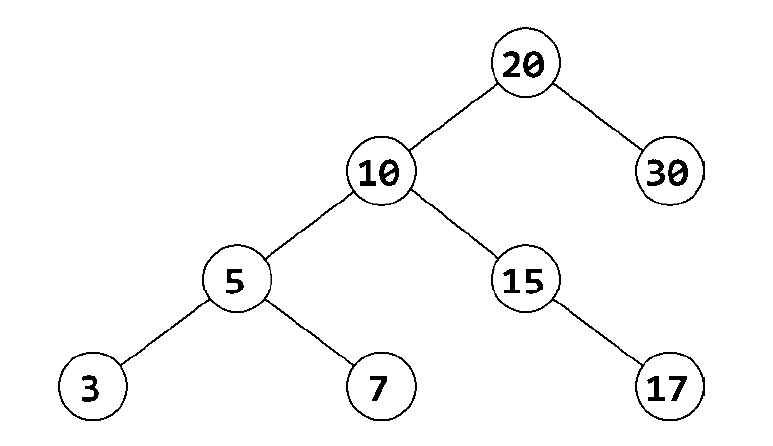
以下面这棵树为例:
首先,从(min = INT_MIN, max = INT_MAX)这个范围开始,根结点显然落在其中。然后处理左子树,检查这些结点是否落在(min = INT_MIN, max = 20)范围内。然后再处理(值为10的结点)右子树,检查结点是否落在(min = 20, max = INT_MAX)范围内。
然后,继续依此遍历整棵树。进入左子树时,更新max。进入右子树时,更新min。只要有任一结点不能通过检查,则停止并返回false。
这种解法的时间复杂度为O(N),其中N为整棵树的结点数。我们可以证明这已经是最佳做法,因为任何算法都必须访问全部N个结点。
因为用了递归,对于平衡树,空间复杂度为O(log N)。在调用栈上,共有O(log N)个递归用,因为递归的深度最大会到这棵树的深度。
该解法的递归实现代码如下:
boolean checkBST(TreeNode n) {
return checkBST(n, Integer.MIN_VALUE, Integer.MAX_VALUE);
}
boolean checkBST(TreeNode n, int min, int max) {
if (n == null) {
return true;
}
if (n.data < min || n.data >= max) {
return false;
}
if (!checkBST(n.left, min, n.data)
|| !checkBST(n.right, n.data, max)) {
return false;
}
return true;
}
记住,在递归算法中,一定要确定终止条件以及结点为空的情况得到妥善处理。
5. 找出二叉查找树中指定结点的“下一个”结点(也即中序后继)
可以假定每个结点都含有指向父结点的连接
回想一下中序遍历,它会遍历左子树,然后是当前结点,接着是右子树。要解决这个问题,必须非常小心,想想具体是怎么回事。
假定我们有一个假想的结点。我们知道访问顺序为左子树,当前结点,然后是右子树。显然,下一个结点应该位于右边。
不过,到底是右子树的哪个结点呢?如果中序遍历右子树,那它就会是接下来第一个被访问的结点,也就是说,它应该是右子树最左边的结点。够简单吧!
但是,若这个结点没有右子树,又该怎么办?这种情况就有点棘手了。
若结点n没有右子树,那就表示已遍访n的子树。我们必须回到n的父结点,记作q。
若n在q的左边,那么,下一个我们应该访问的结点就是q(中序遍历,left -> current ->right)。
若n在q的右边,则表示已遍访q的子树。我们需要从q往上访问,直至找到我们还未完全遍访过的结点x。怎么才能知道还未完全遍历结点x呢?之前从左结点访问至其父结点时,就已碰到了这种情况。左结点已完全遍历,但其父结点尚未完全遍历。
伪码如下:
Node inorderSucc(Node n) {
if (n has a right subtree) {
return leftmost child of right subtree
} else {
while (n is a right child of n.parent) {
n = n.parent; // 往上
}
return n.parent; // 父结点还未遍历
}
}
且慢,如果一路往上遍访这棵树都没发现左结点呢?只有当我们遇到中序遍历的最末端时,才会出现这种情况。也就是说,如果我们已位于树的最右边,那就不会再有中序后继,此时该返回null。
下面是该算法的实现代码(已正确处理结点为空的情况)。
public TreeNode inorderSucc(TreeNode n) {
if (n == null)
return null;
/* 找到右子结点,则返回右子树里
* 最左边的结点*/
if (n.right != null)
return leftMostChild(n.right);
} else {
TreeNode q = n;
TreeNode x = q.parent;
// 向上直至位于左边而不是右边
while (x != null && x.left != q) {
q = x;
x = x.parent;
}
return x;
}
}
public TreeNode leftMostChild(TreeNode n) {
if (n == null) {
return null;
}
while (n.left != null) {
n = n.left;
}
return n;
}
这不是世上最复杂的算法问题,但要写出完美无瑕的代码却有难度。面对这类问题,比较实用的做法是用伪码勾勒大纲,仔细描绘各种不同的情况。
6. 找出二叉树中某两个结点的第一个共同祖先
设计并实现一个算法,找出二叉树中某两个结点的第一个共同祖先。不得将额外的结点储存在另外的数据结构中。注意:这不一定是二叉查找树。
如果是二叉查找树,我们可以修改find操作,用来查找这两个结点,看看路径在哪里开始分叉。可惜,这不是二叉查找树,因此必须另觅他法。
下面假定我们要找出结点p和q的共同祖先。在此先要问个问题,这棵树的结点是否包含指向父结点的连接。
解法1:包含指向父结点的连接
如果每个结点都包含指向父结点的连接,我们就可以向上追踪p和q的路径,直至两者相交。不过,这么做可能不符合题目的若干假设,因为它需要满足以下两个条件之一:(1) 可将结点标记为isVisited;(2) 可用另外的数据结构如散列表储存一些数据。
解法2:不包含指向父结点的连接
另一种做法是,顺着一条p和q都在同一边的链子,也就是说,若p和q都在某结点的左边,就到左子树中查找共同祖先。若都在右边,则在右子树中查找共同祖先。要是p和q不在同一边,那就表示已经找到第一个共同祖先。
这种做法的实现代码如下。
/* 若p为root的子孙,则返回true */
boolean covers(TreeNode root, TreeNode p) {
if (root == null)
return false;
if (root == p)
return true;
return covers(root.left, p) || covers(root.right, p);
}
TreeNode commonAncestorHelper(TreeNode root, TreeNode p, TreeNode q) {
if (root == null)
return null;
if (root == p || root == q)
return root;
boolean is_p_on_left = covers(root.left, p);
boolean is_q_on_left = covers(root.left, q);
/* 若p和q不在同一边,则返回root */
if (is_p_on_left != is_q_on_left)
return root;
/* 否则就是在同一边,遍访那一边*/
TreeNode child_side = is_p_on_left ? root.left : root.right;
return commonAncestorHelper(child_side, p, q);
}
TreeNode commonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (!covers(root, p) || !covers(root, q)) { // 错误检查
return null;
}
return commonAncestorHelper(root, p, q);
}
这个算法在平衡树上的运行时间为O(n)。这是因为第一次调用时,covers会在2n个结点上调用(左边n个结点,右边n个结点)。接着,该算法会访问左子树或右子树,此时covers会在2n/2个结点上调用,然后是2n/4,依此类推。最终的运行时间为O(n)。
至此,就渐近式运行时间(asymptotic runtime)来看,可以确定没有更优解了,因为必须遍访这棵树的每一个结点才行。不过,或许我们还能减小常数倍的值。
解法3:最优化
尽管解法2在运行时间上已经做到最优,还是可以看出部分低效的操作。特别是,covers会搜索root下的所有结点以查找p和q,包括每棵子树中的结点(root.left和root.right)。然后,它会选择那些子树中的一棵,搜遍它的所有结点。每棵子树都会被一再地反复搜索。
你可能会觉察到,只需搜索一遍整棵树,就能找到p和q。然后,就可以“往上冒泡”在栈里找到先前的结点。基本逻辑与上一种解法相同。
使用函数commonAncestor(TreeNode root, TreeNode p, TreeNode q)递归访问整棵树,这个函数的返回值如下:
- 返回p,若root的子树含有p(而非q);
- 返回q,若root的子树含有q(而非p);
- 返回null,若p和q都不在root的子树中;
- 否则,返回p和q的共同祖先。
在最后一种情况下,要找到p和q的共同祖先比较简单。当commonAncestor(n.left, p, q)和commonAncestor(n.right, p, q)都返回非空的值时(意即p和q位于不同的子树中),则n即为共同祖先。
下面的代码提供了初步的解法,不过其中有个bug。试着找找看。
/* 下面的代码有个bug */
TreeNode commonAncestorBad(TreeNode root, TreeNode p, TreeNode q) {
if (root == null) {
return null;
}
if (root == p && root == q) {
return root;
}
TreeNode x = commonAncestorBad(root.left, p, q);
if (x != null && x != p && x != q) { // 已经找到父系结点
return x;
}
TreeNode y = commonAncestorBad(root.right, p, q);
if (y != null && y != p && y != q) { // 已经找到父系结点
return y;
}
if (x != null && y != null) { // 在不同子树里找到p和q
return root; // 这是共同祖先
} else if (root == p || root == q) {
return root;
} else {
/* x或y有一个非空,则返回非空的那个值*/
return x == null ? y : x;
}
}
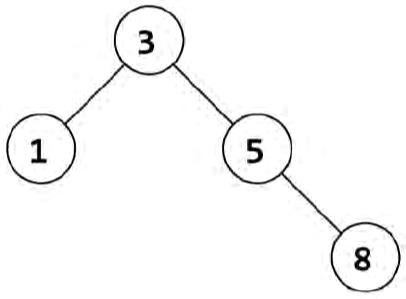
假如有个结点不在这棵树中,这段代码就会出问题。例如,请看下面这棵树:
假设我们调用commonAncestor(node 3, node 5, node 7)。当然,结点7并不存在,而这正是问题的源头。调用序列如下:
commonAncestor(node 3, node 5, node 7) // --> 5
calls commonAncestor(node 1, node 5, node 7) // --> null
calls commonAncestor(node 5, node 5, node 7) // --> 5
calls commonAncestor(node 8, node 5, node 7) // --> null
换句话说,对右子树调用commonAncestor时,前面的代码会返回结点5,这也符合代码本意。问题在于查找p和q的共同祖先时,调用函数无法区分下面两种情况。
- 情况1:p是q的子结点(或相反,q为p的子结点)。
- 情况2:p在这棵树中,而q不在这棵树中(或者相反)。
不论哪种情况,commonAncestor都将返回p。对于情况1,这是正确的返回值,而对于情况2,返回值应该为null。
我们需要设法区分这两种情况,这也是以下代码所做的。这段代码的做法是返回两个值:结点自身,以及指示这个结点是否确为共同祖先的标记。
public static class Result {
public TreeNode node;
public boolean isAncestor;
public Result(TreeNode n, boolean isAnc) {
node = n;
isAncestor = isAnc;
}
}
Result commonAncestorHelper(TreeNode root, TreeNode p, TreeNode q){
if (root == null) {
return new Result(null, false);
}
if (root == p && root == q) {
return new Result(root, true);
}
Result rx = commonAncestorHelper(root.left, p, q);
if (rx.isAncestor) { // 找到共同祖先
return rx;
}
Result ry = commonAncestorHelper(root.right, p, q);
if (ry.isAncestor) { // 找到共同祖先
return ry;
}
if (rx.node != null && ry.node != null) {
return new Result(root, true); // 这是共同祖先
} else if (root == p || root == q) {
/* 若我们当前位于p或q,并发现其中一个结点
* 位于子树中,那么这真的就是一个共同祖先,
* 标记应该设为true。*/
boolean isAncestor = rx.node != null || ry.node != null ? true : false;
return new Result(root, isAncestor);
} else {
return new Result(rx.node!=null ? rx.node : ry.node, false);
}
}
TreeNode commonAncestor(TreeNode root, TreeNode p, TreeNode q) {
Result r = commonAncestorHelper(root, p, q);
if (r.isAncestor) {
return r.node;
}
return null;
}
当然,由于这个问题只会在p或q并不属于这棵树的情况下出现,另一种避免bug的做法是先搜遍整棵树,以确保两个结点都在树中。
7. 判断T2是否为T1的子树
你有两棵非常大的二叉树:T1,有几百万个结点;T2,有几百个结点。设计一个算法,判断T2 是否为T1 的子树。
如果T1 有这么一个结点n,其子树与T2 一模一样,则T2 为T1 的子树。也就是说,从结点n处把树砍断,得到的树与T2 完全相同。
碰到类似的问题,不妨假设只有少量的数据,以此为基础解决问题。这么做很有用,可以借此找出可行的基本解法。
在规模较小且较简单的问题中,我们可以创建一个字符串,表示中序和前序遍历。若T2前序遍历是T1前序遍历的子串,并且T2中序遍历是T1中序遍历的子串,则T2为T1的子树。利用后缀树可以在线性时间内检查是否为子串,因此就最差情况的时间复杂度而言,这个算法是相当高效的。
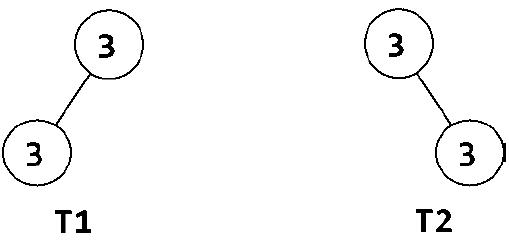
注意,我们需要在字符串中插入特殊字符,表示左结点或右结点为NULL的情况。否则,我们就无法区分以下两种情况:
尽管这两棵树不同,但两者的中序和前序遍历完全一样。
T1,中序:3, 3
T1,前序:3, 3
T2,中序:3, 3
T2,前序:3, 3
不过,要是标记出NULL值,就能区分这两棵树:
T1,中序:0, 3, 0, 3, 0
T1,前序:3, 3, 0, 0, 0
T2,中序:0, 3, 0, 3, 0
T2,前序:3, 0, 3, 0, 0
对于简单的情形,这种解法还算不错,但是我们真正要面对的问题涉及的数据量要大得多。鉴于该问题指定的约束条件,创建两棵树的副本可能要占用太多的内存。
另一种解法
另一种解法是搜遍较大的那棵树T1。每当T1的某个结点与T2的根结点匹配时,就调用treeMatch。treeMatch方法会比较两棵子树,检查两者是否相同。
分析运行时间有点复杂,粗略一看的答案可能是O(nm),其中n为T1的结点数,m为T2的结点数。虽然在技术上这个答案是正确的,但稍微再想想就能得到更靠谱的答案。
我们不必对T2的每个结点调用treeMatch,而是会调用k次,其中k为T2根结点在T1中出现的次数。因此运行时间接近O(n + km)。
其实,即使这样运行时间也有所夸大。即使根结点相同,一旦发现T1和T2有结点不同,我们就会退出treeMatch。因此,每次调用treeMatch,也不见得都会查看m个结点。
下面是该算法的实现代码。
boolean containsTree(TreeNode t1, TreeNode t2) {
if (t2 == null) { // 空树一定是子树
return true;
}
return subTree(t1, t2);
}
boolean subTree(TreeNode r1, TreeNode r2) {
if (r1 == null) {
return false; // 大的树已经空了,还未找到子树
}
if (r1.data == r2.data) {
if (matchTree(r1,r2))
return true;
}
return (subTree(r1.left, r2) || subTree(r1.right, r2));
}
boolean matchTree(TreeNode r1, TreeNode r2) {
if (r2 == null && r1 == null) // 若两者都空
return true; // 子树中已无结点
// 若其中之一为空,但并不同时为空
if (r1 == null || r2 == null) {
return false;
}
if (r1.data != r2.data)
return false; // 结点数据不匹配
return (matchTree(r1.left, r2.left) && matchTree(r1.right, r2.right));
}
}
什么情况下用简单解法比较好,什么时候另一种解法比较好呢?这个问题值得跟面试官好好讨论一番,下面是几点注意事项。
- 简单解法会占用
O(n + m)内存,而另一种解法则占用O(log(n) + log(m))内存。记住:要求可扩展性时,内存使用多寡关系重大。 - 简单解法的时间复杂度为
O(n + m),另一种解法在最差情况下的执行时间为O(nm)。话说回来,只看最差情况的时间复杂度可能会造成误导,我们需要做进一步观察。 - 如前所述,比较准的运行时间为
O(n + km),其中k为T2根结点在T1中出现的次数。假设T1和T2的结点数据为0和p之间的随机数,则k值大约为n / p,为什么?因为T1有n个结点,每个结点有1/p的几率与T2根结点相同,因此,T1中大约有n / p个结点等于T2根结点(T2.root)。举个例子,假设p = 1000,n = 1 000 000且m = 100。我们需要检查的结点数量大致为1 100 000(1100 000 = 1 000 000 + 100*1 000 000/1000)。 - 借助更复杂的数学运算和假设,就能得到更准确的运行时间。在第3点中,我们假设调用treeMatch时将遍历T2的全部m个结点。然而,更有可能出现的情况是,我们很早就发现两棵树有不同的结点,然后提早就退出了这个函数。
总的来说,在空间使用上,另一种解法显然比较好,在时间复杂度上,也可能比简单解法更优。一切都取决于你做出哪些假设,以及要不要考虑牺牲最差情况的运行时间,来减少平均情况的运行时间。这一点非常值得向面试官提出并讨论。
8. 打印二叉树节点数值和等于给定数值的所有路径
给定一棵二叉树,其中每个结点都含有一个数值。设计一个算法,打印结点数值总和等于某个给定值的所有路径。注意,路径不一定非得从二叉树的根结点或叶结点开始或结束。
下面我们运用简化推广法来解题。
部分1:简化——假设路径必须从根结点开始,但可以在任意结点结束,怎么解决?
在这种情况下,问题就会变得容易很多。
我们可以从根结点开始,向左向右访问子结点,计算每条路径上到当前结点为止的数值总和,若与给定值相同则打印当前路径。注意,就算找到总和,仍要继续访问这条路径。为什么?因为这条路径可能继续往下经过a + 1结点和a - 1结点(或其他数值总和为0的结点序列),完整路径的总和仍然等于sum。
例如,若sum = 5,可能会得到以下路径:
p = {2, 3}
q = {2, 3, -4, -2, 6}
如果找到2 + 3就停下来,我们就会错过第二条路径,还可能错过其他路径。因此,我们必须继续往下查找所有可能的路径。
部分2:推广——路径可从任意结点开始。
现在,如果路径可从任意结点开始,该怎么办?在这种情况下,我们可以稍作调整。对于每个结点,我们都会向“上”检查是否得到相符的总和。也就是说,我们不再要求“从这个结点开始是否会有总和为给定值的路径”,而是关注“这个结点是否为总和为给定值的某条路径的末端”。
递归访问每个结点n时,我们会将root到n的完整路径传入该函数。随后,这个函数会以相反的顺序,从n到root,将路径上的结点值加起来。当每条子路径的总和等于sum时,就打印这条路径。
public void findSum(TreeNode node, int sum, int[] path, int level) {
if (node == null) {
return;
}
/* 将当前结点插入路径*/
path[level] = node.data;
/* 查找以此为终点且总和为sum的路径*/
int t = 0;
for (int i = level; i >= 0; i--){
t += path[i];
if (t == sum) {
print(path, i, level);
}
}
/* 查找此结点之下的结点*/
findSum(node.left, sum, path, level + 1);
findSum(node.right, sum, path, level + 1);
/* 从路径中移除当前结点。严格来说并不一定要这么做,
* 直接忽略这个值即可,但这么做是个好习惯*/
path[level] = Integer.MIN_VALUE;
}
public void findSum(TreeNode node, int sum) {
int depth = depth(node);
int[] path = new int[depth];
findSum(node, sum, path, 0);
}
public static void print(int[] path, int start, int end) {
for (int i = start; i <= end; i++) {
System.out.print(path[i] + “ “);
}
System.out.println();
}
public int depth(TreeNode node) {
if (node == null) {
return 0;
} else {
return 1 + Math.max(depth(node.left), depth(node.right));
}
}
那么,这个算法的时间复杂度如何(假设是棵平衡二叉树)?如果结点在r层,那么就需要r份量的工作(向“上”检查结点的步骤)。我们可以猜测时间复杂度为O(n log(n)),因为总共有n个结点,平均下来,每一步需要log(n)的工作量。
如果这么分析,你还是看不大明白,我们也可以用严格的数学推导来说明。注意,在r层上有 个结点。
注意,,因此,
按照同样的逻辑,可以推导出算法的空间复杂度为O(log(n)),因为该算法会递归O(log n)次,而在递归调用中参数path只分配一次空间(大小为O(log n))。