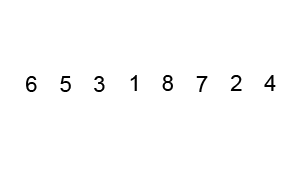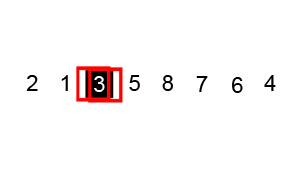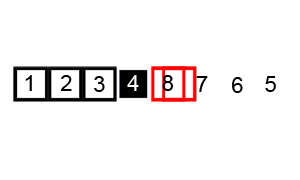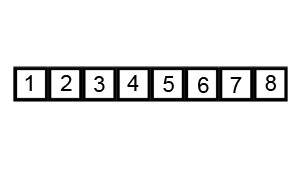数据结构面试题：数组

1. 在一个给定的从1到100的整型数组中，如何快速找到缺失的数字

如元素无重复，缺失一个数字时可采用下面方法：

二分法：假设有序，如无需先排序，二分查找，时间复杂度 O(logN)。

求和法：1到100之和 - 数组数字之和 = 缺失数字，时间复杂度： O(n)，空间复杂度： O(1)。

异或法：依次位异或1到100，然后继续位异或数组所有数字，结果即为缺失数字，时间复杂度： O(n) ，空间复杂度： O(1)。

Hash法：对数组数据Hash，可以使用BitSet，时间复杂度 O(n) ，空间复杂度 O(n) 。

扩展1：数组中缺失两个数

先排序，然后将原数据拆分成两部分，使用原始问题方法即可。

如求min~max之和 S1，数组元素和 S2，设缺失元素为 a、b，则 S1-S2 = a+b，以 (a+b)/2 为界将排序后的原数据拆分成两部分，问题即变为原始问题。

扩展2：范围1到100，99个出现了偶数次，1个奇数次，求奇数次的数

数组全部元素位异或，结果即为所求。

扩展3：范围1到100，98个出现了偶数次，2个奇数次，求奇数次的数

设两个出现奇数次的数分别为a、b，则数组全部元素位异或结果 c 等于 a^b，则 c 中至少有一位为1（如无则说明两个数相等，不符合题意）。

接着对 c 进行分析，如果 c 中某一位为1，则说明 a、b 两个数在此位上一个为0，一个为1，因此以此位为界，将原数据分成两部分，问题即变为扩展2。

例如范围1~5的原始数据 [1, 3, 2, 5, 4, 2, 6, 6, 3, 5]，全部位异或后 c=5=a^b，二进制为 0101，如将最低位1作为界对原数据分成 [1, 3, 5, 3, 5] 和 [2, 4, 2, 6, 6] 两部分，求最低位1的方法 c-(c&(c-1))，此时使用扩展2方法即可。

2. 如何在不使用Java Collection API的情况下从数组中删除重复项

先排序，然后遍历移除连续出现的重复数据，可直接在原数组上将重复数据置为0（假设原数据中没有0），或者借助临时数组。

3. 在一个未排序的整型数组中，如何找到最大和最小的数字

定义max、min分别保存数值范围的最小值及最大值，循环比较并记录max、min的值即可。

4. 找出一个数组中的两个数字，使这两个数字之和等于一个给定的值

方法一：

直接穷举，从数组中任意取出两个数字，计算两者之和是否为给定的数字。显然其时间复杂度为 O(n(n-1)/2) 即 O(n^2)。

方法二：

使用Hash表，根据Hash表映射查找一个数字是否存在。遍历数组，使用给定值减去数组元素，接着拍段差值是否存在于Hash表中，时间复杂度可降为 O(n)，但会根据数组元素的取值范围使用过大的存储空间。

方法三：

首先对数组进行排序，时间复杂度为 O(n*log2n)。然后令 i=0，j=n-1，判断 arr[i]+arr[j] 是否等于给定数字，如果是则 arr[i]、arr[j]即为所求。如果小于给定数字则 i+=1，否则 j-=1。这样只需在排序后的数组上遍历一次，就可求得结果，时间复杂度为 O(n)。两步加起来总的时间复杂度 O(n*log2n)。

5. 如果一个数组包含多个重复元素，如何找到这些重复的元素

方法一：

使用二重循环两两比较得到重复元素，时间复杂度为 O(n^2)。

for (int i = 0; i < names.length; i++) {
    for (int j = i + 1 ; j < names.length; j++) {
        if (names[i].equals(names[j])) {
            // 得到重复元素
        }
    }
}

方法二：

使用Set，因为Set不允许插入重复元素，可通过add()的返回值判断元素是否重复，时间复杂度为 O(n)。

for (String name : names) {
    if (set.add(name) == false) {
        // 得到重复元素
    }
}

方法三：

使用哈希表，遍历数组元素通过数组元素值与元素数量构建哈希表，再遍历哈希表输出数量非1的元素即为重复元素。这种方法时间复杂度为 O(n)，与方法二相同，但却能够准确求到重复数量。

// 构造哈希表
for (String name : names) {
    Integer count = nameAndCount.get(name);
    if (count == null) {
        nameAndCount.put(name, 1);
    } else {
        nameAndCount.put(name, ++count);
    }
}

// 打印重复元素以及重复数量
Set<Entry<String, Integer>> entrySet = nameAndCount.entrySet();
for (Entry<String, Integer> entry : entrySet) {
    if (entry.getValue() > 1) {
        System.out.printf("duplicate element '%s' and count '%d' :", entry.getKey(), entry.getValue());
    }
}

6. 用Java从一个给定数组中删除重复元素

方法一：

不借助数据结构，申请一个跟给定数组一样大小的新数组，遍历给定数组将给定数组中的每一个元素放入新数组中，放入时遍历新数组判断是否已存在，时间复杂度为 O(n^2)。

方法二：

使用List的contains，本质上跟方法一一样。

int[] attr = { 1, 2, 3, 3, 5, 5, 7, 9 };
List<Integer> list = new ArrayList<Integer>();
for (int i : attr) {
    if (!list.contains(i)) {
        list.add(i);
    }
}

方法三：

使用Set或LinkedHashSet，特别是LinkedHashSet，因为它能够保持元素是有序的，时间复杂度为 O(n)。

方法四：

先排序再遍历放入新数组中，可根据数组有序的特性快速过滤掉重复元素，时间复杂度由排序算法决定。

7. 如何利用快速排序对一个整型数组进行排序

快速排序过程如下。

import java.util.Arrays;

public class QuickSortDemo{
    public static void main(String args[]) {
        // unsorted integer array
        int[] unsorted = {6, 5, 3, 1, 8, 7, 2, 4};
        System.out.println("Unsorted array :" + Arrays.toString(unsorted));

        QuickSort algorithm = new QuickSort();

        // sorting integer array using quicksort algorithm
        algorithm.sort(unsorted);

        // printing sorted array
        System.out.println("Sorted array :" + Arrays.toString(unsorted));
    }
}

class QuickSort {
    private int input[];
    private int length;

    public void sort(int[] numbers) {
        if (numbers == null || numbers.length == 0) {
            return;
        }
        this.input = numbers;
        length = numbers.length;
        quickSort(0, length - 1);
    }

    /*
     * This method implements in-place quicksort algorithm recursively.
     */
    private void quickSort(int low, int high) {
        int i = low;
        int j = high;

        // pivot is middle index
        int pivot = input[low + (high - low) / 2];

        // Divide into two arrays
        while (i <= j) {
            /**
             * As shown in above image, In each iteration, we will identify a
             * number from left side which is greater then the pivot value, and
             * a number from right side which is less then the pivot value. Once
             * search is complete, we can swap both numbers.
             */
            while (input[i] < pivot) {
                i++;
            }
            while (input[j] > pivot) {
                j--;
            }
            if (i <= j) {
                swap(i, j);
                // move index to next position on both sides
                i++;
                j--;
            }
        }

        // calls quickSort() method recursively
        if (low < j) {
            quickSort(low, j);
        }

        if (i < high) {
            quickSort(i, high);
        }
    }

    private void swap(int i, int j) {
        int temp = input[i];
        input[i] = input[j];
        input[j] = temp;
    }
}

Output :
Unsorted array :[6, 5, 3, 1, 8, 7, 2, 4]
Sorted array :[1, 2, 3, 4, 5, 6, 7, 8]

8. 用 Java 实现数组反转

数组第一个元素与最后一个元素交换，第二个元素与倒数第二个元素交换，时间复杂度为 O(n/2)或O(n)，空间复杂度O(1)。